Premessa: a me la matematica piace, sarà che mi dà un senso di incastro perfetto, di tutto-sotto-controllo, di se-ti-applichi-ce-la-puoi-fare, di assenza di trucchi, di pulizia, un po' come la corsa. E poi sia la matematica che la corsa sono attività minimaliste, bastano un paio di scarpe per l'una e neanche quelle per l'altra. Tuttavia non sono un runner professionista, e ancora meno un matematico; nel corso degli anni passati ne ho studiato qualche aspetto (della matematica, non della corsa) ma sempre da testi alla portata di tutti (a parte un paio di esami piuttosto generici all'università). Per il resto faccio un mestiere che consiste nell'analisi di aspetti quantitativi di fenomeni, quindi ha a che fare con i numeri, ma niente di più complesso delle quattro operazioni combinate in vario modo. Diciamo che sono un Pivello a cui piace leggere di matematica, parlare di matematica ai figli e cercare di incasellare le cose che vede in schemi quanto più possibile logico/matematici. Pertanto vi chiedo venia sin d'ora per quello che segue, che a un Vero Matematico (1) sembrerà probabilmente un discreto mucchio di ingenuità presentate con ottima improprietà di linguaggio. E questo tanto per essere a posto con la coscienza.
Vorrei riprendere un argomento che ho trattato tempo fa ma che non sono ancora riuscito a digerire, e che continuerò a riproporvi di tanto in tanto fino a quando qualcuno non sarà riuscito a spiegarlmelo in maniera a me comprensibile. Si tratta di una formuletta che mi ha sempre lasciato esterrefatto, che mette in relazione tra loro cinque elementi tra i basilari della matematica e che è conosciuta come l'Identità di Eulero. E' questa roba qui:
Ha l'aspetto innocuo, riuscirebbe a leggerla persino un bimbo di quinta elementare, ma nasconde un segreto a me inaccessibile.
Provo innanzitutto a presentare i protagonisti della formula, i magnifici cinque:
1 è il primo numero naturale, l'elemento neutro della moltiplicazione, l'Unità carica di significati filosofici, credo esista da quando esiste un linguaggio. E' anche il titolo del primo disco dei Led Zeppelin. Insomma, mi pare importante.
0 è l'elemento neutro dell'addizione, l'unico numero ad essere né positivo né negativo e ad essere citato in ben tre assiomi su cinque nel sistema di Peano (ne ho parlato qui qualche tempo fa). Fu introdotto dai matematici indiani attorno al settimo secolo e neanche lui scherza in quanto a fama.
e è la costante conosciuta come numero di Nepero; si tratta della base della funzione esponenziale (scelta in modo che la derivata dell'esponenziale sia uguale alla esponenziale stessa) e, di conseguenza, base dei logaritmi naturali, funzione inversa dell'esponenziale. E' irrazionale, quindi non è esprimibile né come frazione né come numero decimale se non con infinite cifre dopo la virgola, è approssimabile a 2,71828 ed è una delle costanti più famose, fin da quando nel seicento il matematico scozzese Nepero la utilizzò per la prima volta nella sua opera sui logaritmi.
π è l'arcinoto rapporto tra una circonferenza e il suo diametro, probabilmente la costante più utilizzata in assoluto in matematica, è anch'essa irrazionale ed è pari a circa 3,14159. Era conosciuta sin dall'antichità, credo che i primi a utilizzarla, anche se non con la precisione odierna, siano stati i babilonesi 4 mila anni fa.
i è l'unità immaginaria, il numero complesso che elevato al quadrato dà come risultato -1. I numeri complessi furono introdotti a fatica tra il sedicesimo e il diciottesimo secolo per trovare soluzioni ad equazioni tipo x2 + 1 = 0. Non è nemmeno esprimibile come numero decimale.
Cinque elementi che attraversano temporalmente secoli di storia, introdotti per rispondere alle esigenze più varie, che appartengono a branche completamente diverse del grande caleidoscopio di cultura che mettiamo sotto il nome di matematica, di primo acchitto si direbbe che non c'entrino nulla l'uno con l'altro.
 E invece c'è questa identità semplice semplice, facile facile, talmente corta che potrebbe essere tatuata su un lobo, che le mette tutte insieme e che dice: prendi un numero reale che serve come base dei logaritmi, elevalo al rapporto tra la circonferenza e il suo diametro moltiplicato per l'unità immaginaria, poi aggiungici l'elemento neutro della moltiplicazione, vedrai che il tutto farà... ZERO!
E invece c'è questa identità semplice semplice, facile facile, talmente corta che potrebbe essere tatuata su un lobo, che le mette tutte insieme e che dice: prendi un numero reale che serve come base dei logaritmi, elevalo al rapporto tra la circonferenza e il suo diametro moltiplicato per l'unità immaginaria, poi aggiungici l'elemento neutro della moltiplicazione, vedrai che il tutto farà... ZERO! E' un po' come se provassi a preparare il tiramisù seguendo la ricetta della zia, e quando metti insieme con fiducia il mascarpone e i Pavesini alla fine quello che ottieni è il vuoto assoluto. Come per magia tutto quello che metteva paura al Pivello (l'unità immaginaria che non si riesce ad immaginare, le infinite cifre dopo la virgola, l'elevamento a potenza di roba che non si capisce) svanisce nel nulla, annichilisce come in un rendez-vous di materia e antimateria, delle infinite cifre non rimane che il ricordo (2), l'unità immaginaria va a fare loro compagnia, e rimane lo zero. Questo per me è un mistero.

tutto giusto, ci mancherebbe, Eulero avrà fatto le cose per bene, ma questo non toglie nulla alla mia sorpresa. Non toglie nulla alla sensazione di Magia.
E' questo che mi affascina: nonostante io non lo comprenda, posso ragionevolmente credere che funzioni.
Vado a farmi un tatuaggio sul lobo.
- cfr Roberto Zanasi
- Se provate a elevare e alla π si ottiene 23,14058. C'è qualche Vero Matematico disposto a spiegare a un Pivello dova va a finire questa roba?
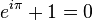
Ehi, veri matematici, non vi affollate! O il sig. Tacchino sarà costretto a moderare i commenti.
RispondiEliminaSecondo me furbeggi e sai benissimo perché l'identità di Eulero dà zero. Io no.
RispondiEliminaCiao!
Sei in buona compagnia.
EliminaNella ricetta l'elemento neutro lo devi aggiungere e non togliere, altrimenti è come fare il tiramisù senza caffè, che pure dev'essere buono :-)
RispondiEliminaHo corretto il caffè, grazie per la segnalazione.
EliminaAggiungi al tiramisù un bimbo goloso ed otterrai zero.
RispondiEliminaDevopensarcisu
Uh, prova qui: http://proooof.blogspot.it/2010/07/la-formula-piu-bella-della-matematica.html
RispondiEliminaGrazie Zar, mi ero già imbattuto in questo approccio di tipo geometrico sul piano complesso, ma ti confesso che è fuori dalla mia portata. Mi fermo al mio stupore dal punto di vista algebrico. Ho invece letto recentemente una meravigliosa dimostrazione che un numero irrazionale elevato ad un numero irrazionale può dare come risultato un numero razionale, e questo mi ha fatto fare un teorico passo avanti. Mah, vedremo.
RispondiElimina