ZenThree, ovvero come misurare

Abbiamo capito qualche giorno fa, ed esclusivamente grazie a questo blog, come si conta. Poi abbiamo imparato a contare fino ad infinito. Ora che sappiamo maneggiarli, con questi numeri cerchiamo di farci qualcosa di più concreto; per esempio potremmo misurare qualcosa.
E' quello che si è fatto con i numeri dall'alba dei tempi: dopo il semplice atto di contare degli oggetti distinti (di solito le mele) si è cercato di sfruttarne le potenzialità per misurare qualunque cosa fosse a portata di mano, la capacità di un recipiente, l'area di un campo, la larghezza di un fiume, la lunghezza di un organo genitale. Se non fossero stati adatti a misurare, probabilmente alla fine i numeri non sarebbero durati un gran che come concetto.
E allora vediamo se i numeri più semplici, quelli naturali (1, 2, 3, ecc.), sono adatti a questo scopo. Si potrebbe di primo acchitto pensare di sì, voglio dire, potremmo stabilire una unità di misura non troppo grande, ad esempio un metro, e misurare con quello e con i suoi multipli interi quello che ci pare. Per un campo ok, per un fiume pure, ma per l'organo dovremmo utilizzare qualcosa di più piccolo, almeno se prendo a spunto la mia esperienza. Beh, per misurare le cose più piccole possiamo usare le parti di un metro, ossia le sue frazioni: mezzo metro, un decimetro, un centimetro, o addirittura un milionesimo di metro. Ma sì, pergiove, posso scegliere la frazione che voglio, e con quella riuscirò a misurare in maniera esatta proprio tutto!!!Quando i pitagorici si accorserò che le cose non stavano così, letteralmente sbroccarono. Come è possibile che per quanto sia piccola la frazione di una qualsiasi unità di misura che prendo in considerazione, ci sono cose che non riesco a misurare?
Ad esempio prendiamo una figura semplicissima, un quadrato con il lato di un metro. Se ne volessi misurare la diagonale mi accorgerei che un metro è poco, ma che due sono troppo; quindi faccio delle frazioni, prendo i centimetri e mi accorgo che 141 centimetri sono pochi e che 142 sono troppi; allora prendo i millimetri, ma 1414 sono pochi e 1415 troppi, allora mi incazzo e prendo i miliardesimi di metro ma 1414213562 sono pochi, 1414213563 troppi, e mi viene da piangere. E' proprio quello che fecero i pitagorici quando si accorsero che per quanto avessere preso frazioni minuscole non sarebbero mai riusciti a misurare una semplice diagonale di un semplice fottutissimo quadrato.
All'inizio pensandoci stavo sbroccando anch'io, ho anche pensato che l'inghippo dipendesse dal sistema decimale; mi dicevo, beh, se lo scriviamo in sistema binario o esadecimale risolviamo la questione, poi mi sono imbattuto nella dimostrazione matematica qui sotto che come molte dimostrazioni ha di bello che è indipendente dalla notazione che usi, parla di costanti e variabili e rapporti tra di loro, e come Montalbano mi sono fatto persuaso.
Ad esempio.
Prendiamo il problema del quadrato. Abbiamo studiato a scuola che se un quadrato ha un metro di lato, la sua diagonale è facilissima da calcolare, grazie al teorema del capostipite degli sbroccati, ed è semplicemente la radice quadrata di due, ossia quel numero che elevato al quadrato da 2 come risultato.
Ma c'è questa semplice dimostrazione che dice che la radice quadrata di 2 (che indichiamo come , ora faccio anche i simboli in maniera più umana, tiè) è un numero irrazionale, che significa non esprimibile tramite una frazione, un rapporto di due numeri interi.
La dimostrazione è molto bella, nel senso che se esiste un concetto di bello assoluto al mondo credo che questa cosa ci si avvicini parecchio, allo stesso livello con il clavicembalo ben temperato di Bach e con la notte stellata di Van Gogh.
Fa più o meno così: si supponga che sia razionale, ovvero che sia possibile esprimerlo sotto forma di rapporto tra due numeri interi m ed n, ossia la frazione , già ridotta ai minimi termini.
Quindi  .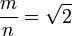
Se eleviamo entrambi i membri al quadrato otteniamo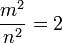
ovvero  m² = 2n²
Il termine 2n² è pari (perchè è un numero moltiplicato per 2), pertanto anche m² è pari, e conseguentemente m stesso dev'essere pari (il quadrato di un numero dispari è sempre dispari), quindi esiste un opportuno k tale per cui m = 2k. Sostituendo, si ottiene:

2n² = (2k)²

che, sviluppando il quadrato e semplificando, diventa

n² = 2k²

Con identico ragionamento, essendo ora 2k² pari si deduce che anche n², e quindi n stesso, siano a loro volta pari.
Sia m che n risultano pertanto essere pari, il che contraddice l'ipotesi iniziale che sia irriducibile: se ne conclude che non è esprimibile sotto forma di frazione, e che quindi la nostra ipotesi iniziale è falsa. Dunque abbiamo dimostrato l'opposto, cioè che è irrazionale.
Tutta questa cosa significa che il numero non si potrà mai esprimere come rapporto tra due numeri interi, indipendentemente dal sistema numerico che utilizziamo per scriverlo.
La conseguenza notevole, quella che sconvolse i pitagorici, è che, oltre ai numeri razionali, che sono infiniti, esistono altri infiniti numeri irrazionali completamente diversi dai razionali.
Un infinito dentro ad un altro infinito.
Mi pare sufficiente per un post.